本网讯（通讯员杨新宇）11月13日晚，瑞典哥德堡大学Graham Leigh 教授通过网络平台作了题为“证明，真和验证（Proof, Truth and Verification）”的讲座，旨在介绍劣基证明论(ill-founded proof theory)的基本思想和当前进展。讲座由我院程勇教授主持，伯明翰大学Anupam Das教授评议，线上参与者近200人次。

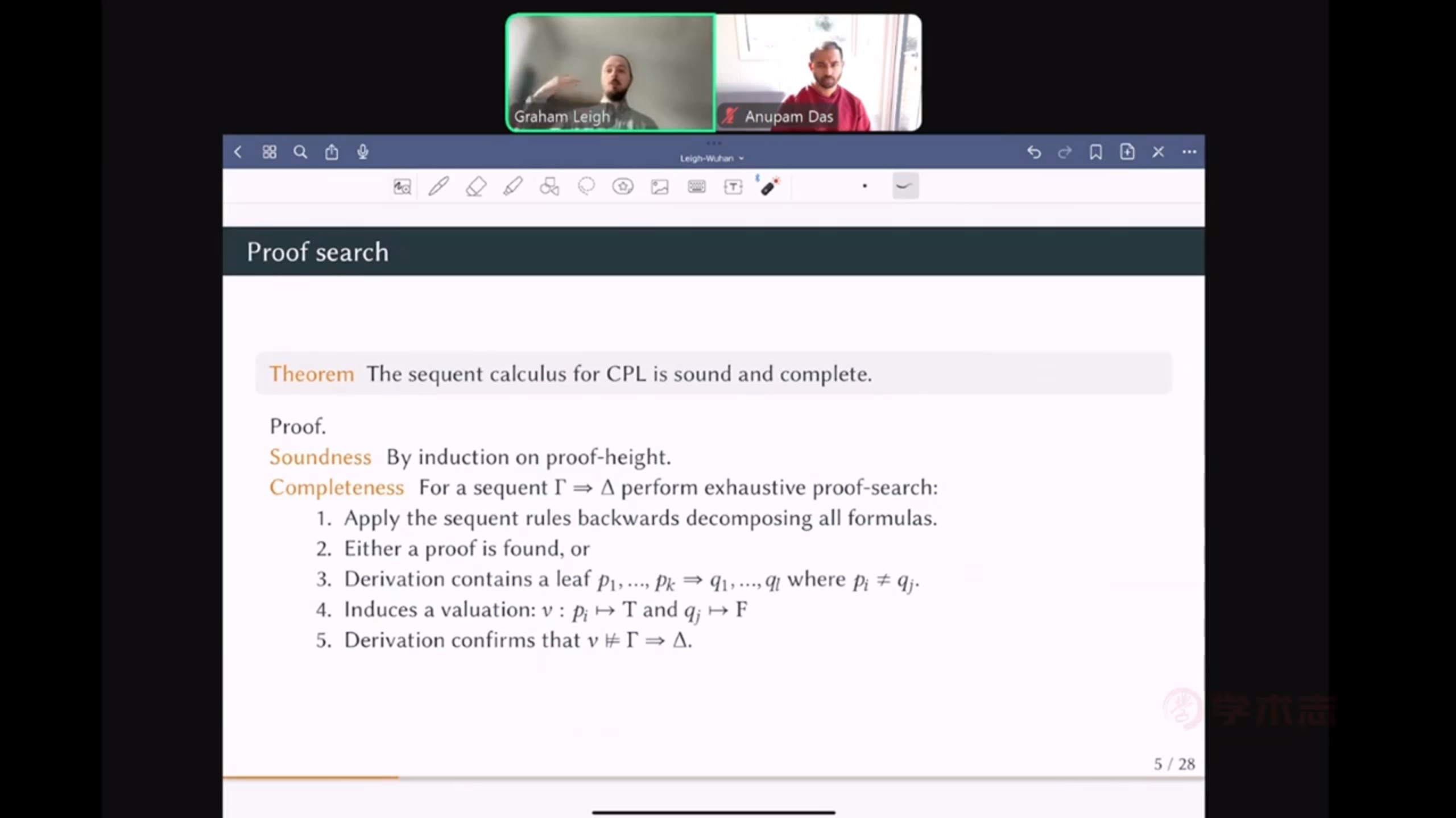
Leigh教授首先回顾了命题逻辑的矢列演算(sequential calculus)系统CPL，这一系统具有可靠性和完全性，对于可靠性的证明可以通过施归纳于证明的高度，对于完全性的证明则是通过证明搜索(proof search)的技术证明，即通过对一个矢列的公式分解，我们要么可以得到该矢列的在系统中的一个证明，要么可以构造出不满足该序列的一个真值指派。CPL的另一个重要性质是一些规则的可允许性(admissibility)。通过证明变换(proof transform)的方法我们不仅可以证明CPL初始规则的逆规则是递归地可允许的，还可以证明切割(cut)规则是递归地可允许的，这就是著名的切割-消除（cut-elimination）定理。切割-消除具有很好的性质，逻辑学家Mints在1978年证明了切割-消除可以看作是推演空间上的连续算子。

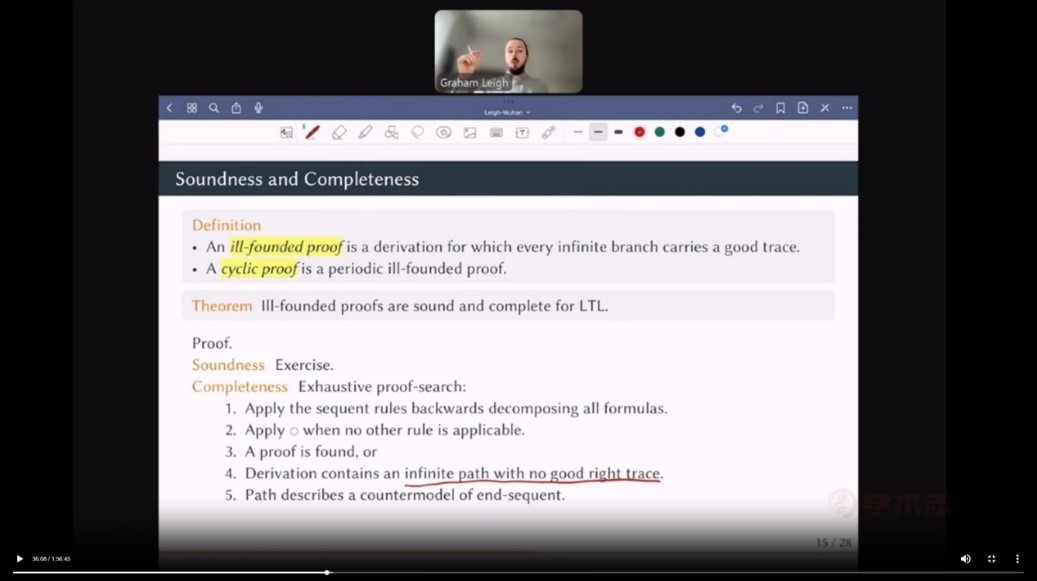
讲座的第二部分是余-归纳(co-inductive)证明论。劣基证明(ill-founded proof)的概念很自然地出现在不同的逻辑和理论系统中，如线性时态逻辑和皮亚诺算术中。这类证明具有很好的性质：证明变换是连续的；证明的复杂性而非大小是其主要指标；便于系统的模块化分析。Leigh教授以线性时态逻辑和皮亚诺算术为例对其进行了介绍。线性时态逻辑有两类算子：表示命题从现在开始一直为真的算子和表示命题在下一个时刻为真的算子。通过对一个典型的线性时态逻辑证明搜索的分析，Leigh教授引入了迹(trace)和优迹(good trace)的概念，进而形式地定义了劣基证明和循环证明。通过证明搜索的方法可以证明线性时态逻辑的劣基证明系统是可靠且完全的，通过证明变换的方法可以证明切割规则在线性时态逻辑的递归可允许性。另一个重要的例子则是皮亚诺算术PA。皮亚诺算术的矢列演算系统是在CPL的基础上添加量词规则、等词规则和归纳规则、切割规则扩展而成的。通过对更强的           算术（将归纳规则替换为有无穷多个前提的ω规则）的证明论刻画，我们可以给出PA的序数分析：任何PA可证矢列在           算术中有不使用切割规则的高度小于序数          的证明。然        算术中的证明不具备很多良好的性质：缺少计算复杂性的信息；无法扩展到其他系统；不具备模块化性质。另外一种思路是重新定义量词规则，引入算术的劣基证明系统和循环证明系统。可以证明，算术的劣基证明系统强度上和真算术等价，而循环证明系统和PA等价。同时可以用和线性时态逻辑类似的方法证明劣基证明系统的切割消除定理，由此可知无切割证明不可能是循环的。

讲座的最后一部分是劣基证明和序数分析之间的联系。通过定义切割迹(cut trace)，我们可以对劣基证明指派序数。逻辑学家Afshari的研究表明，在二阶算术的一个子系统上，可以证明对某个推演的序数的超穷归纳蕴含该推演的最复杂的切割规则可以被消除。这个子系统需要多强呢？Leigh教授猜想这一结论在WKL₀（弱Koing引理系统）上可证。不仅如此，通过劣基证明的切割消除的精细分析，我们有可能在WKL₀+          直到序数          的超穷归纳)上给出PA一致性的新证明。此外，这一领域当前仍有许多未解决的问题：比如对其他的理论（如归纳定义的形式理论）的劣基证明论分析。

在讲座的讨论环节，Anupam Das教授就这一领域许多未解问题的技术细节，如归纳定义的理论和高阶逻辑的劣基证明论，和Leigh教授进行了广泛深入地交流。荷兰莱顿大学的Göran Sundholm教授就ω算术的证明搜索向Leigh教授分享了看法，程勇教授就哥德尔第二不完全性定理的一个推论——不存在有穷的无切割的矢列演算系统刻画PA与Leigh教授进行了讨论。此外，线上的观众则就原始递归算术和WKL₀的强度比较及逻辑学家Gentzen关于PA的一致性证明和这里提到的一致性证明的关联和Leigh教授进行了交流。

最后程勇教授感谢Leigh教授带来的精彩讲座，至此，本场讲座完满结束。

（编辑：邓莉萍 审稿：刘慧）